Wegfindung mit A*
Dieser Artikel muss noch verbessert werden! Bitte hilf uns dabei!
Näheres dazu findest du auf der Diskussionsseite. Wenn die dort beschriebenen Mängel behoben sind, kannst du diesen Hinweis entfernen.
A* (A Stern) ist ein Algorithmus, um einen kürzesten oder kostengünstigsten Weg zwischen zwei Punkten zu finden. Dafür verwendet er eine Schätzfunktion, die dazu beiträgt gerichtet zu suchen, was im Allgemeinen die Effizienz der Suche verbessert. Gibt es einen Weg zwischen den zwei Punkten, so ist garantiert, dass A* ihn auch findet. Weiterhin ist garantiert, dass immer ein kürzester Weg gefunden wird.
Inhaltsverzeichnis |
Verwendung
Im Prinzip kann A* überall da verwendet werden, wo Spielobjekte (z.B. die Spielfigur oder Gegner) von A nach B gelangen müssen und dabei eigenständig ihren Weg finden sollen.
| Genre | Spielevertreter | im Detail |
|---|---|---|
| Echtzeitstrategie | Command and Conquer | eigene/gegnerische Einheiten |
| rundenbasiertes Strategiespiel | Civilization | eigene/gegnerische Einheiten |
| Ego-Shooter | Half Life | gegnerische Einheiten |
| MMORPG | World of Warcraft | eigene Begleiter / gegnerische Einheiten |
Wichtige Bestandteile von A*
Hier wird auf die wichtigsten Komponenten des Algorithmus eingegangen, weil diese Begriffe später immer wieder auftauchen.
Die Knoten
Als Knoten wird in diesem Zusammenhang ein Punkt auf dem Spielfeld bezeichnet. Ein Knoten kann, muss aber keine geometrische Form aufweisen. Diese Knoten können auch nur abstrakt existieren.
A* unterscheidet zwischen verschiedene Arten von Knoten:
- unbekannte Knoten
- bekannte Knoten
- untersuchte Knoten
Ein unbekannter Knoten muss dem A*-Algorithmus erst im Laufe der Zeit bekannt gemacht werden. Bekannte Knoten können untersucht werden. Durch diese Untersuchung können unbekannte Knoten entdeckt werden. Diese unbekannten Knoten werden analysiert und werden zu bekannten Knoten. Wenn der bekannte Knoten einmal untersucht wurde, bleibt es dabei, und er wird nicht noch einmal untersucht. Allerdings können bekannte Knoten wiederholt analysiert werden.
Die Schätzfunktion
Die Schätzfunktion wird benötigt, um dem aktuell untersuchten Knoten einen Wert zu zuweisen. Dieser Wert macht darüber eine Aussage, wie weit der Knoten schätzungsweise vom Ziel entfernt ist. Die Schätzfunktion wird im Allgemeinen als §h§ bezeichnet (für Heuristik), und die geschätzten Kosten nennen wir §H§.
Es gibt verschiedene Ansätze für die Schätzfunktion, und es hängt auch immer davon ab, was im Spiel genau erreicht werden soll. Wichtig ist jedoch, dass die geschätzten Kosten nie größer sein dürfen als die tatsächlichen Kosten. Die Schätzfunktion darf die Kosten also nicht überschätzen.
Eine einfache Schätzfunktion ist die direkte Distanz zwischen dem aktuellen Knoten und dem Ziel. Diese Distanz wird mittels des Satz des Pythagoras ermittelt.
Eine weitere Möglichkeit ist die Manhattan-Distanz. Bei dieser Methode werden vom entstehenden Dreieck einfach die Längen der beiden Katheten addiert. Diese darf aber nur dann angewendet werden, wenn keine diagonalen Bewegungen erlaubt sind, ansonsten würde sie die Kosten überschätzen. Ihren Namen hat diese Distanzfunktion aus dem New Yorker Stadtteil Manhattan, da man sich dort normalerweise nur vertikal und horizontal durch die Straßen um die Gebäudeblöcke bewegen kann.
Nach Pythagoras:
§Distanz = \sqrt{{x_{Laenge}}^2 + {y_{Laenge}}^2} = \sqrt{5^2 + 8^2} = 9.4 §
Manhattan-Distanz:
§Distanz = x_{Laenge} + y_{Laenge} = 5 + 8 = 13 §
Die Werte F, G und optionale Werte
Eng verbunden mit der Schätzfunktion sind zwei weitere Werte. Der Wert für den bereits zurückgelegten Weg vom Startknoten wird im Allgemeinen als §G§ bezeichnet. Ein weiterer wichtiger Wert ist die Summe aus §H§ und §G§. Dieser Wert wird §F§ genannt. Er stellt später das Suchkriterium dar, nach dem aus der Openlist ein Knoten ausgewählt wird.
Es gibt auch weitere Werte, die auf den Algorithmus einen Einfluss haben können. Zum Beispiel Extrakosten, die bei Strategiespielen durch unwegsames Gelände zustande kommen. Eine weitere Möglichkeit sind auch Drehbewegung einer Spielfigur, die ebenfalls Kosten verursachen können.
Diese "optionalen Werte" sollten auch mit in die Rechnung für §F§ einfließen.
Berechnungsformel: §F = H + G + Optional§
Die Openlist
In die Openlist kommen alle Knoten die bekannt sind. Bei der Openlist kann es sich um eine Verkettete Liste oder ein Array handeln. In dieser List können die Knoten nach ihren F werten sotiert werden. Somit kann schneller auf den erfolgversprechendsten Knoten zugegriffen werden.
Die Closedlist
In die Closedlist kommen alle Knoten die bereits untersucht wurden. Bei diese Liste handelt es sich ebenfals um eine verkettete Liste oder ein Array. Die Reihenfolge in der Closedlist spielt keine Rolle.
Arbeitsweise von A*
Hier wird jetzt beschrieben wie alle Komponenten des Algorithmus zusammen arbeiten.
Datenstruktur eines Knoten
Diese Werte sollte ein Knoten mindestens speichern können.
- H - Beinhaltet den Schätzwert
- G - Zurückgelegte Wegkosten
- F - Summe aus G und H
- Coord_X - x-Koordinate des Knotens
- Coord_Y - y-Koordinate des Knotens
- ComeFrom_X - x-Koordinate des Knotens, von dem auf den aktuellen Knoten zugegriffen wurde
- ComeFrom_Y - y-Koordinate des Knotens, von dem auf den aktuellen Knoten zugegriffen wurde
Vielleicht auch noch zwei zusätzliche Flags:
- isOpenList
- isClosedList
Das erspart dann Rechenzeit aufwendige Vergleiche zwischen den beiden Listen, ob ein Knoten schon in der Closedlist ist.
Beschreibung
Zu begin sind nur 2 Knoten dem Algorithmus bekannt, der Startknoten und der Zielknoten. Der Startknoten wird der Openlist zugefügt. Den Zielknoten behalten wir erstmal nur im Hinterkopf.
In der Openlist wird nun nach dem geeignetesten Knoten gesucht. Da hier nur der Startknoten drin steht fällt die Wahl nicht schwer. Jetzt wird der Startknoten untersucht, das bedeutet das nach allen benachbarten Knoten gesucht wird. Für jeden gefundenen Knoten werden die Werte für H, G und F ermittelt. Die ermittelten Werte werden natürlich in den jeweiligen Knoten gespeichert. Weiterhin muss auch gespeichert werden, von welchem Knoten man auf den neuen Knoten gekommen ist. Die neu gefunden Knoten werden alle in die Openlist eingefügt. Der Startknoten wird von einem bekannten Knoten zu einem untersuchten Knoten und wird damit in die ClosedList eingefügt.
Jetzt wird in der Openlist nach dem Knoten gesucht der den geringsten F Wert hat. Von diesem Knoten werden nun wieder alle benachbarten Knoten gesucht und analysiert. Dabei kann es vorkommen das im laufe der Zeit Knoten die schon in der Openlist stehen nochmal analysiert werden. Wenn der F wert sich verbessert sollten alle Daten des Knoten Überschrieben werden. Sind die Daten gleich oder schlechter können die alten Daten beibehalten werden.
So arbeitet der Algorithmus die Openlist ab, fügt unbekannte Knoten der Openlist zu und fügt untersuchte Knoten der Closedlist zu. Wenn jetzt der Zielknoten der Closedlist zugefügt wird ist es vollbracht. Der günstigste weg ist gefunden.
Nun kann ausgehend vom Zielknoten geschaut werden von welchem Knoten man auf den Zielknoten kamm. Von dem wird dann geschaut von welchem Knoten man auf diesen kamm und immer so weiter bis man wieder am Startknoten angekommen ist. So wird dann der beste Weg abgebildet.
Wenn die Openlist leer ist bevor man den Zielknoten erreicht hat kann der Algorithmus abgebrochen werden, da dann kein Weg zwischen Start- und Zielnoten existiert.
Schritt für Schritt mit Bildern
Da Bilder bekanntlich mehr sagen als 1000 Worte, noch einmal alles in Bildern erklärt.
Die Rahmenbedingungen für den Algorithmus:
- Keine diagonalen Schritte erlaubt
- Schätzfunktion durch Manhattan-Methode ermittelt
- 1 Schritt Kostet 1 Punkt
- Richtungswechsel kostet 1 Punkt (in Tabelle Spalte Z)
- Knotennamen sind die x- und y-Koordinaten
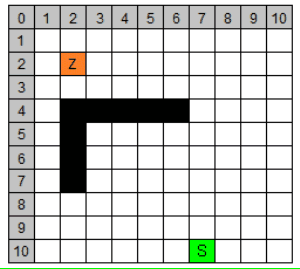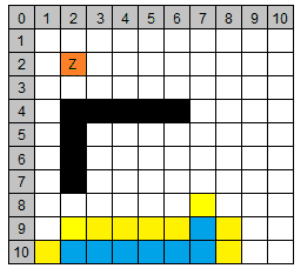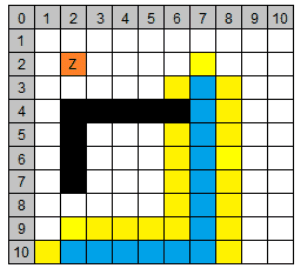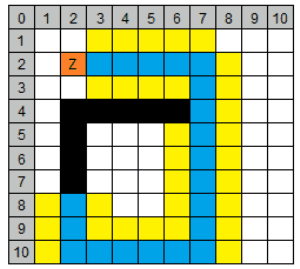
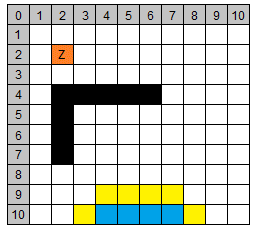
Spielfeld-Legende:
- grün: Startpunkt (7/10)
- orange: Zielpunkt (2/2)
- weiß: unbekannte Knoten
- gelb: bekannte Knoten (Openlist)
- blau: untersuchte Knoten (Closedlist)
- schwarz: nicht begehbare Knoten
| Openlist | Closedlist | |||||||
| Schritt | Knotenname | H | G | Z | F | Bild | Knotenname | ComeFrom |
|---|---|---|---|---|---|---|---|---|
| 1 | (7/10) | 13 | 0 | 0 | 13 |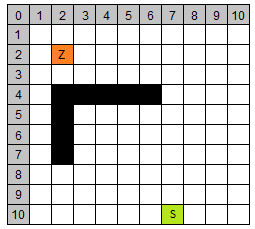 
|
N/A | N/A |
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
| Schritt | Knotenname | H | G | Z | F | Bild | Knotenname | ComeFrom |
|---|---|---|---|---|---|---|---|---|
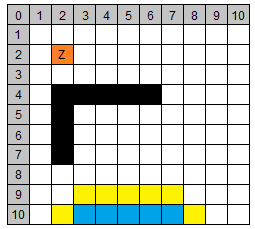
| 2 | (6/10) | 12 | 1 | 0 | 13 |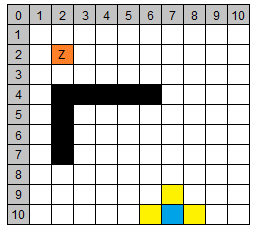 
|
(7/10) | N/A |
| (7/9) | 12 | 1 | 0 | 13 | ||||
| (8/10) | 14 | 1 | 0 | 15 | ||||
| 2 | ||||||||
| 2 | ||||||||
| 2 | ||||||||
| 2 | ||||||||
| 2 | ||||||||
| 2 |
| Schritt | Knotenname | H | G | Z | F | Bild | Knotenname | ComeFrom |
|---|---|---|---|---|---|---|---|---|
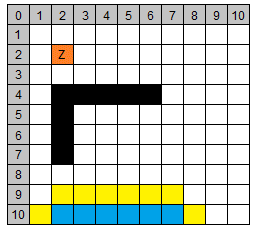
| 3 | (5/10) | 11 | 2 | 0 | 13 |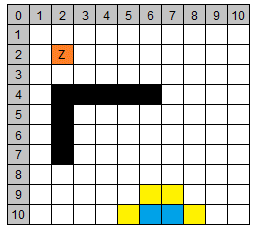 
|
(7/10) | N/A |
| 3 | (7/9) | 12 | 1 | 0 | 13 | (6/10) | (7/10) | |
| 3 | (6/9) | 12 | 2 | 1 | 15 | |||
| 3 | (8/10) | 14 | 1 | 0 | 15 | |||
| 3 | ||||||||
| 3 | ||||||||
| 3 | ||||||||
| 3 | ||||||||
| 3 |
| Schritt | Knotenname | H | G | Z | F | Bild | Knotenname | ComeFrom |
|---|---|---|---|---|---|---|---|---|
| 4 | (4/10) | 10 | 3 | 0 | 13 |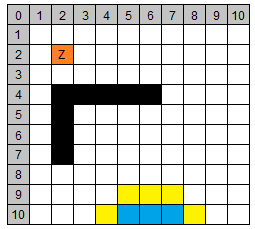 
|
(7/10) | N/A |
| 4 | (7/9) | 12 | 1 | 0 | 13 | (6/10) | (7/15) | |
| 4 | (5/9) | 11 | 3 | 1 | 15 | (5/10) | (6/10) | |
| 4 | (6/9) | 12 | 2 | 1 | 15 | |||
| 4 | (8/10) | 14 | 1 | 0 | 15 | |||
| 4 | ||||||||
| 4 | ||||||||
| 4 | ||||||||
| 4 |
| Schritt | Knotenname | H | G | Z | F | Bild | Knotenname | ComeFrom |
|---|---|---|---|---|---|---|---|---|
| 5 | (3/10) | 9 | 4 | 0 | 13 | 
|
(7/10) | N/A |
| 5 | (7/9) | 12 | 1 | 0 | 13 | (6/10) | (7/10) | |
| 5 | (4/9) | 10 | 4 | 1 | 15 | (5/10) | (6/10) | |
| 5 | (5/9) | 11 | 3 | 1 | 15 | (4/10) | (5/10) | |
| 5 | (6/9) | 12 | 2 | 1 | 15 | |||
| 5 | (8/10) | 14 | 1 | 0 | 15 | |||
| 5 | ||||||||
| 5 | ||||||||
| 5 |
| Schritt | Knotenname | H | G | Z | F | Bild | Knotenname | ComeFrom |
|---|---|---|---|---|---|---|---|---|
| 6 | (2/10) | 8 | 5 | 0 | 13 | 
|
(7/10) | N/A |
| 6 | (7/9) | 12 | 1 | 0 | 13 | (6/10) | (7/10) | |
| 6 | (3/9) | 9 | 5 | 1 | 15 | (6/10) | (5/10) | |
| 6 | (4/9) | 10 | 4 | 1 | 15 | (4/10) | (5/10) | |
| 6 | (5/9) | 11 | 2 | 1 | 15 | (3/10) | (4/10) | |
| 6 | (6/9) | 12 | 2 | 1 | 15 | |||
| 6 | (8/10) | 14 | 1 | 0 | 15 | |||
| 6 | ||||||||
| 6 |
| Schritt | Knotenname | H | G | Z | F | Bild | Knotenname | ComeFrom |
|---|---|---|---|---|---|---|---|---|
| 7 | (7/9) | 12 | 1 | 0 | 13 | 
|
(7/10) | N/A |
| 7 | (2/9) | 8 | 6 | 1 | 15 | (6/10) | (7/10) | |
| 7 | (3/9) | 9 | 5 | 1 | 15 | (6/10) | (5/10) | |
| 7 | (1/10) | 9 | 6 | 0 | 15 | (4/10) | (5/10) | |
| 7 | (4/9) | 10 | 4 | 1 | 15 | (3/10) | (4/10) | |
| 7 | (5/9) | 11 | 3 | 1 | 15 | (2/10) | (3/10) | |
| 7 | (6/9) | 12 | 2 | 1 | 15 | |||
| 7 | (8/10) | 14 | 1 | 0 | 15 | |||
| 7 |
...
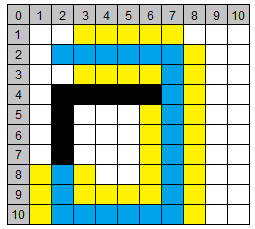
Wer üben will, kann Schritt 8 und folgende anhand der Animation selber ausprobieren. Wir springen jetzt gleich zum letzten Schritt, um zu zeigen, wie man nun den Weg abgehen kann.
| Schritt | Knotenname | H | G | Z | F | Bild | Knotenname | ComeFrom |
|---|---|---|---|---|---|---|---|---|
| 21 | (6/3) | 5 | 8 | 1 | 14 | 
|
(7/10) | N/A |
| (6/5) | 7 | 6 | 1 | 14 | (6/10) | (7/10) | ||
| (3/9) | 8 | 5 | 1 | 14 | (6/10) | (5/10) | ||
| (6/6) | 8 | 5 | 1 | 14 | (4/10) | (5/10) | ||
| (4/9) | 9 | 4 | 1 | 14 | (3/10) | (4/10) | ||
| (6/7) | 9 | 4 | 1 | 14 | (2/10) | (3/10) | ||
| (5/9) | 10 | 3 | 1 | 14 | (7/9) | (7/10) | ||
| (6/8) | 10 | 3 | 1 | 14 | (7/8) | (7/9) | ||
| (6/9) | 11 | 2 | 1 | 14 | (7/7) | (7/8) | ||
| (7/1) | 6 | 9 | 0 | 15 | (7/6) | (7/7) | ||
| (1/10) | 9 | 6 | 0 | 15 | (7/5) | (6/7) | ||
| (8/10) | 14 | 1 | 0 | 15 | (7/4) | (7/5) | ||
| (8/2) | 6 | 9 | 1 | 16 | (7/3) | (7/4) | ||
| (8/3) | 7 | 8 | 1 | 16 | (7/2) | (7/3) | ||
| (8/4) | 8 | 7 | 1 | 16 | (2/9) | (2/10) | ||
| (8/5) | 9 | 6 | 1 | 16 | (2/8) | (2/9) | ||
| (8/6) | 10 | 5 | 1 | 16 | (6/2) | (7/2) | ||
| (8/7) | 11 | 4 | 1 | 16 | (5/2) | (6/2) | ||
| (8/8) | 12 | 3 | 1 | 16 | (4/2) | (5/2) | ||
| (8/9) | 13 | 2 | 1 | 16 | (3/2) | (4/2) | ||
| (3/1) | 2 | 13 | 2 | 17 | (2/2) | (3/2) | ||
| (3/3) | 2 | 13 | 2 | 17 | ||||
| (4/1) | 3 | 12 | 2 | 17 | ||||
| (4/3) | 3 | 12 | 2 | 17 | ||||
| (5/1) | 4 | 11 | 2 | 17 | ||||
| (5/3) | 4 | 11 | 2 | 17 | ||||
| (6/1) | 5 | 10 | 2 | 17 | ||||
| (1/8) | 7 | 8 | 2 | 17 | ||||
| (3/8) | 7 | 8 | 2 | 17 | ||||
| (1/9) | 8 | 7 | 2 | 17 |
In der ClosedList steht jetzt schon der richtige Weg, zwar ist er nicht in der richtigen Reihenfolge, aber das stört nicht. Wenn man jetzt beim Zielknoten (2/2) in die Spalte ComeFrom schaut, steht dort ein Knoten (3/2). Jetzt sucht man sich in der Spalte Knotenname diesen Knoten heraus. In dieser Reihe steht unter ComeFrom wieder ein Knoten, und so "hangelt" man sich die Liste entlang bis man zum Startknoten kommt.
Der Weg, den der Algorithmus abgeht, sieht dann so aus:
(2/2) -> (3/2) -> (4/2) -> (5/2) -> (6/2) -> (7/2) -> (7/3) -> (7/4) -> (7/5) -> (7/6) -> (7/7) -> (7/8) -> (7/9) -> (7/10)
